Вариант задания | Формулировка задачи |
1. | Пройдет ли кирпич со сторонами x, y, z сквозь прямоугольное отверстие со сторонами r и s. Стороны отверстия должны быть параллельны граням кирпича. |
2. | Можно ли коробку размером a ´ b ´ c упаковать в посылку размером r ´ s ´ t? «Углом» укладывать нельзя. |
3. | Можно ли из круглой заготовки радиуса r вырезать две прямоугольные пластинки с размерами a ´ b и c ´ d? |
4. | Лежит ли точка M(xm, ym) внутри треугольника, заданного координатами своих вершин A(xA, yA), B(xB, yB), C(xC, yC)? |
5. | Путник двигался t1 часов со скоростью v1, а затем t2 часов – со скоростью v2и t3 часов – со скоростью v3. За какое время он одолел первую половину пути, после чего запланировал привал? |
6. | Проверить лежит ли окружность 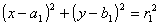
целиком внутри окружности 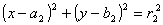 и наоборот. и наоборот. |
7. | Можно ли на прямоугольном участке застройки размером a на b метров разместить два дома размером p на q и r на s метров? Дома можно располагать только параллельно сторонам участка. |
8. | Дано число x. Выести в порядке возрастания числа: sin x, cos x, ln x. Если при каком либо x некоторые из выражений не имеют смысла, вывести сообщение об этом и сравнивать значения только тех, которые имеют смысл. |
9. | Даны три положительных числа. Определить, можно ли построить треугольник с длинами сторон, равным этим числам. Если можно, то ответить на вопрос, является ли он остроугольным. |
10. | По заданным трем числам определить, является ли сумма каких-либо из них положительной. |
11. | Даны действительные числа a, b, c. Удвоить эти числа, если a < b <c, и заменить их абсолютными значениями, если это не так. |
12. | Осуществить перевод величин из радианной меры в градусную и наоборот. Программа должна запрашивать, какой перевод нужно осуществить, и выполнять указанное действие. |
13. | Определить будут ли прямые A1x+B1y+C1 и A2x+B2y+C2 перпендикулярны. Если нет, то найти угол между ними. |
14. | Известно, что из четырех чисел a1, a2, a3 и a4 одно отлично от трех других, равных между собой; присвоить номер этого числа переменной n. |
15. | Даны три точки A(x1,y1), B(x2,y2) и C(x3,y3). Определить, будут ли они расположены на одной прямой. Если нет, то вычислить угол Ð ABC. |
16. | Написать программу решения уравнения ax3+bx=0 для произвольных a,b. |
17. | Даны три положительных числа a, b, c. Проверить, могут ли они быть длинами сторон треугольника. Если да, то вычислить его площадь. |
18. | В доме M этажей и всего один подъезд; на каждом этаже по 3 квартиры; лифт может останавливаться только на нечетных этажах. Человек садится в лифт и набирает номер нужной ему квартиры N. На каком этаже остановится лифт? |
19. | Написать программу решения системы линейных уравнений  |
20. | Проверить, не приводит ли к переполнению суммирование двух целых чиселA и B (т.е. к результату большему, чем 32767). Если переполнение, сообщить об этом, если нет – вывести сумму. |